技艺

浮点数在计算机中的表示

接上一篇博客《为什么会有补码？》，我仅仅分析了整数在计算机中表示方式，但是计算机中的浮点数又是如何表示的呢？

bridge-8291058_1920.jpg

引子

首先，使用之前博客的程序，可以看到如下的这些实数在计算机中的计算结果是

实际数值 数值类型 计算机中的表示
102.3235 float 42CCA5A2
-3.256 float C050624E
120.254 double 405E104189374BC7
-56.2441 double C04C1F3EAB367A10

右边的计算机中的数值表示是按照《IEEE 754-2008》的标准存储数据的，具体的规定如下所示。

IEEE 754 标准

表示形式

IEEE 754规定了二进制浮点数在计算中的存储方式，我们以C语言中的float为例来具体说明。无论是32位系统还是64位系统，计算机中的float占用4个字节，我们就使用这些字节来存储任意的浮点数，可以参考下图

转化成对应的数学表示形式，浮点数 V

$$ V = (-1)^s\times M\times 2^E $$

  • s 表示符号位，占据1个bit 位，如果是负数则s=1，如果是非负数则s=0；
  • M表示尾数，占据23个比特，表示有效数字，表示的数字介于1和2之间；
  • E为直属，表示基于2为基数的指数大小，占据8个比特。

因此，如果确认了上面3个参数，也就唯一确定了浮点数在计算机中的存储形式。我们以 102.3235为例，来看看上面的这几个数字是如何表示出来的？

  1. 102.3235的二进制原码形式是 1100110.01010010110100001110 = 1.10011001010010110100001110*2^6；
  2. 确认s。因为是正数，因此 s=0。
  3. 确认M。M表示 1.xxxxxx之后的 xxxxxx的部分，即计算机内部保存M时，默认表示的第一位总是 1，可以舍弃表示 1 的这一位，而仅仅存储小数点之后的部分。因此 M=10011001010010110100001110，因为只能存储23个比特，将多余的位数部分截断得到M=10011001010010110100001。
  4. 确认E。它是个非负正数，按照第1步计算出来的结果，我们的指数应该是6。但是，IEEE规定根据二进制计算浮点数时，需要给指数减去一个偏置值，对于float类型这个数为127，对于double类型，这个数是1023。因此反过来，在将数字转换成二进制存储的时候，要加上这个偏置值，因此 E=6+127=133。
  5. 综合以上的所有计算结果，最后在计算机中存储的形式是 01000010110011001010010110100001，转换成16进制就是 42CCA5A2。

特别规定

依照上面的方法，可以依次确认其他3个浮点数的表示形式。这都是比较常规的规格化数据的处理方法，IEEE针对一些特殊的数字（绝对值特别接近0的数字或者无穷大无穷小），引入了一些特殊的规定，称为非规格化表示方法，总结如下。

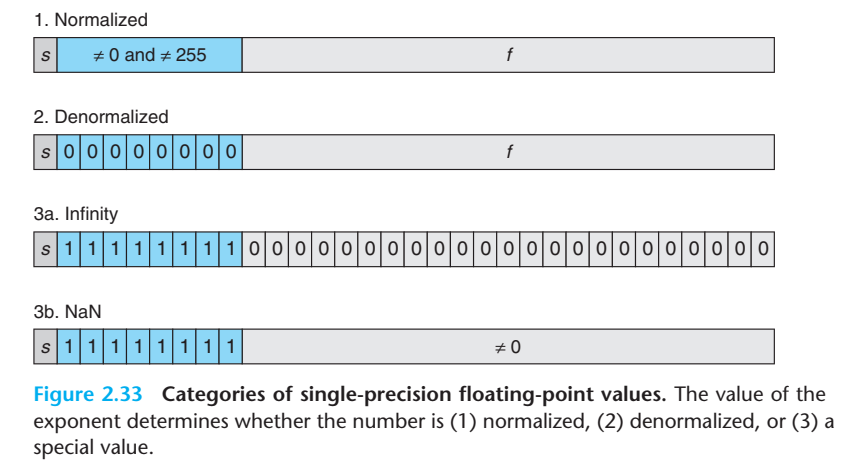
image.png

上一个章节介绍的是规格化的数据，除此之外，还有非规格化的数据和特殊的数据，总结如下

  • 规格化数据。如果指数部分既不是0也不是255（指数部分既不全为0或者不全为1），就是规格化存储方式，具体的计算方法与之前介绍的相同。此时$E = e - Bias$，这里的$e$是指数位宽$w$二进制比特对应的无符号整数，$Bias = 2^{w-1} - 1$，$M = 1.0 + f$。

  • 非规格化数据。指数全为0 就是非规格化的数据。此时$E = 1 - Bias$，$Bias$的值与规格化的相同，$M = f$。很明显，规格化数据不能表示0，非规格化的数据可以，而且0有两种表示。

  • 特殊数字。指数全为1 表示特殊的数字

    • 如果$f$全为0，表示无穷大，正负取决于符号$s$，分别表示$+\infty$和$-\infty$；
    • 如果$f$不为0，表示这是一个非数NaN(Not a Number)。

float16的浮点表示

参考半精度浮点数，基于上面的理解，我们可以研究下float16的一些特点。float16是用16个bit表示浮点数，不同的bit位的表示如下

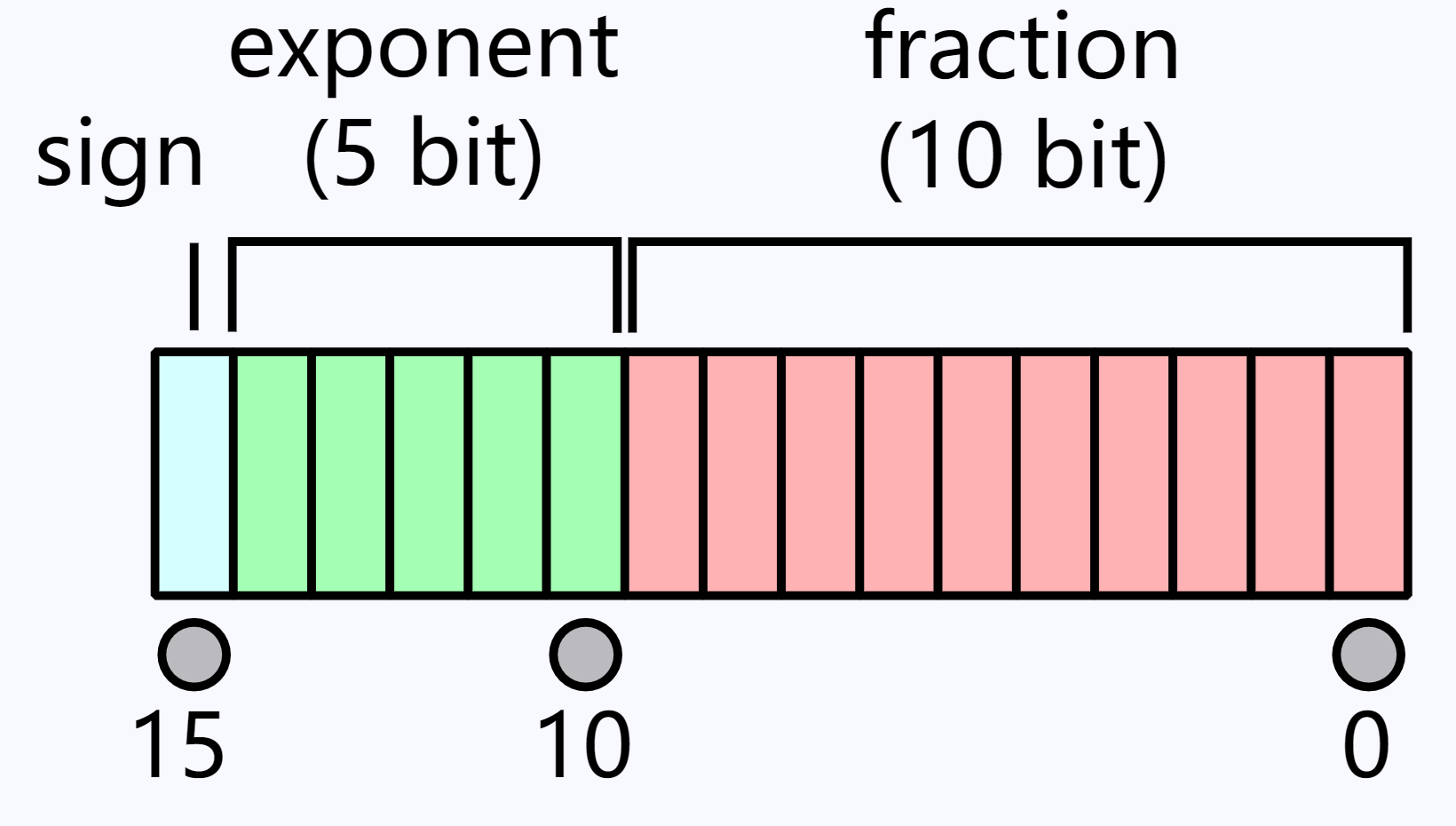
因为负数和正数的值除了符号之外是对称的，所以我们仅仅研究所有的整数表示即可，将16位比特从0到$2^{16}-1$的比特逐个写出来，可以看到如下的表格

说明 二进制比特 $E$ $M$ 准确值($M \times 2^E$) 十进制数
最小非规格化数 0000000000000000 -14 $0\times 2^{-10}$ $0.0 \times 2^{-15}$ 0.0
0000000000000001 -14 $1\times 2^{-10}$ $1\times 2^{-10}\times 2^{-14}$ $6\times 10^{-8}$
0000000000000010 -14 $2\times 2^{-10}$ $2\times 2^{-10}\times 2^{-14}$ $1\times 10^{-7}$
0000000000000011 -14 $3\times 2^{-10}$ $3\times 2^{-10}\times 2^{-14}$ $2\times 10^{-7}$
最大非规格化数 0000001111111111 -14 $(2^{10}-1)\times 2^{-10}$ $(2^{10}-1)\times 2^{-10}\times 2^{-14}= 2^{-14}-2^{-24}$ $6\times 10^{-5}$
最小规格化数 0000010000000000 -14 $1 + 0 \times 2^{-10}$ $2^{-14}$ $6.104\times 10^{-5}$
0000010000000001 -14 $1 + 1 \times 2^{-10}$ $2^{-14}+2^{-24}$ $6.11\times 10^5$
1 0011110000000000 0 $1+0\times 2^{-10}$ $1$ $1$
最大规格化数 0111101111111111 15 $1+(2^{10}-1)\times 2^{-10}$ $(2-2^{-10})\times 2^{15}$ $65500$
无穷大 0111110000000000 – – – $+\infty$

观察上面的表格，可以得到如下的一些结论：

  1. 相对于数学上无穷多的实数，计算机可以精确表示的实数只有有限多个，半精度浮点数可以最多表示$2^{16}$个数，float最多表示$2^{32}$个数等。

  2. 数字在数轴上的表示，越靠近0，可以表示浮点数的越稠密，相应的精度也越高，最高精度是在靠近0的非规格化数里面。假设指数的位宽是$k$bit，位数的位宽是$n$比特，那么最高精度为$\epsilon = 2^{-n}\times 2^{2-2^{k-1}}= 2^{2-n-2^{k-1}}$，可以看出，k和n越长，精度越高，相对于n，k是精度的关键因素。下图是一个按照IEEE的标准的8bit位宽的浮点数表示图（1个bit符号位，3bit是指数位，4bit尾数位），明显可以看到在0的附近表示的数字越稠密。使用ctrl和鼠标中键放大之后，可以看到在0附近的浮点数是均匀分布的。

  3. 从数字0开始，有连续$2\times 2^{n} = 2^{n+1}$个数是等差数列，数列的公差是$\epsilon$，这些数就是$e = [0000\dots0]$和$e=[000\dots01]$的那些数，也就是$E = 1-Bias$的这些数。如果将它们标示在数轴上，它们是最靠近0的那部分区域，这些点均匀分布在这一块区域；

  4. 0和1都可以精确表示，而且因为符号有+-两个符号，所以0有两种表示。

  5. 最大非规格化数和最小化规格数相差一个$\epsilon$，这个差值与非规格数的之间的差值相同，二者平滑过渡。

  6. 可以表示的最大规格化数是$(1-2^{-n-1})\times 2^{2^{k-1}}$;

  7. 如果将二进制比特看成u16的数，那么这些数本身表示的u16的数据大小与它们表示的float的大小关系相同，都是递增的。

下面的代码可以将所有的半精度浮点数的所有非负数表示出来（严格得说，不包括-0.0），可以都打印出来体会下上面的结论

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np

udata = np.uint16(0)
p1 = [] # all of non-negative float16 number
for i in range(2**15):
    p1.append(udata.view(np.float16))
    udata += 1
    udata = np.uint16(udata)

参考资料

comments powered by Disqus