技艺

新冠检测后面的数学定理

新冠检测的科学原理。

混合检测的数学原理

当前居家检测的新冠是10人一组或者20人一组进行混检的，为何不是挨个检测？

检测现状

英国城市利物浦在2020年11月20日刚结束一场大规模的新冠检测项目，这是英国第一次在一个城市做大规模检测。利物浦是英格兰新冠死亡率最高的地区，每百万人感染率是英格兰平均水平约2倍，所以被选为试点。这个试点项目被看作是全英的希望，要在2021年1月之后在英格兰全境推广。但是进度很不理想，原本的目标是在两周内对利物浦全部50万人口进行检测。但两周结束，目标才达成了一半不到，共检测了约20万人，检出来约2000名阳性，600名无症状感染者。所以检测效率是1.42万人次/天。

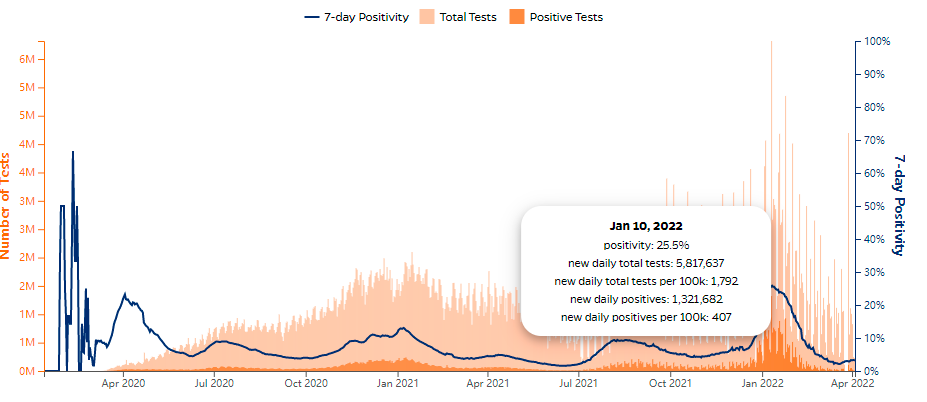
上面是约翰霍普金斯大学的美国每日核酸检测的统计数据，可以看到从2020年4月份到现在，核酸检测的峰值是580万人次/天左右。参考4月4日上海全市核酸检测的速度，2500万人次/天，相差甚远！

混检效率

如果在27个检测样本中有1个阳性样本，如何以比较少的操作将它检测出来？下面是《自然》杂志给出的新冠病毒几种不同的混检方法

方法一

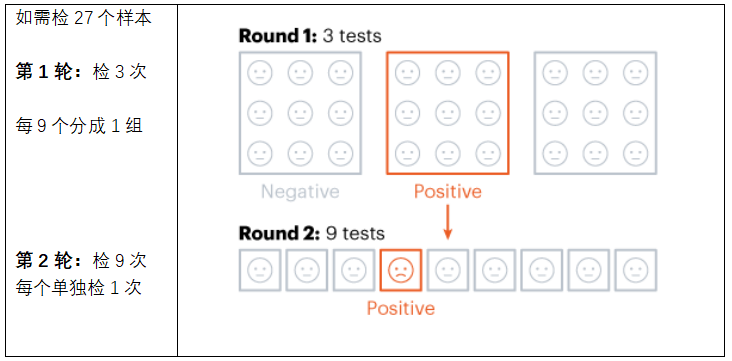
这个也是当前上海核酸检测普遍使用的方法，总计检测次数是3 + 9 = 12次。这种方法最早是由哈佛大学经济学家Robert Dorfman在20世纪40年代提出的，当时是用于检测二战士兵中有多少人携带梅毒。后来也常被用于筛查无症状人群有多少人携带比如衣原体和淋病病毒。红十字会也会用这种方法来筛查献血者中是否有人携带乙肝、艾滋病毒等。该方法的特点是操作简单，检测轮数较少。

方法二

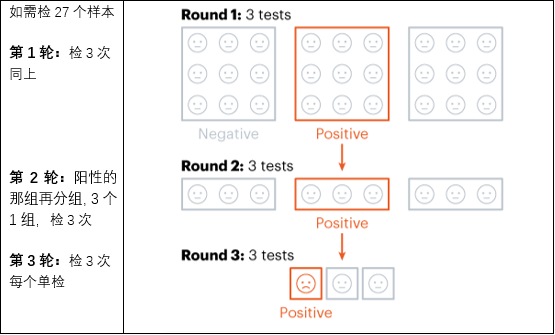
可以称为方法一的改进版，但是与上面相比，总计检测次数是9次，但是真正检出阳性的轮次更多，如果每轮的检测结果都需要等好久，会导致时间拖很长。而且叫人回来检测3次，也有操作上的难度。

方法三

这个是升维的测试方法，第二轮检测按照行检测3次，再按照列检测3次，总计检测次数是3 + 6 = 9次。但是这个方法实际操作比较复杂，如果有不止一个阳性的时候，需要依靠算法来计算哪些是阳性样本。

方法四

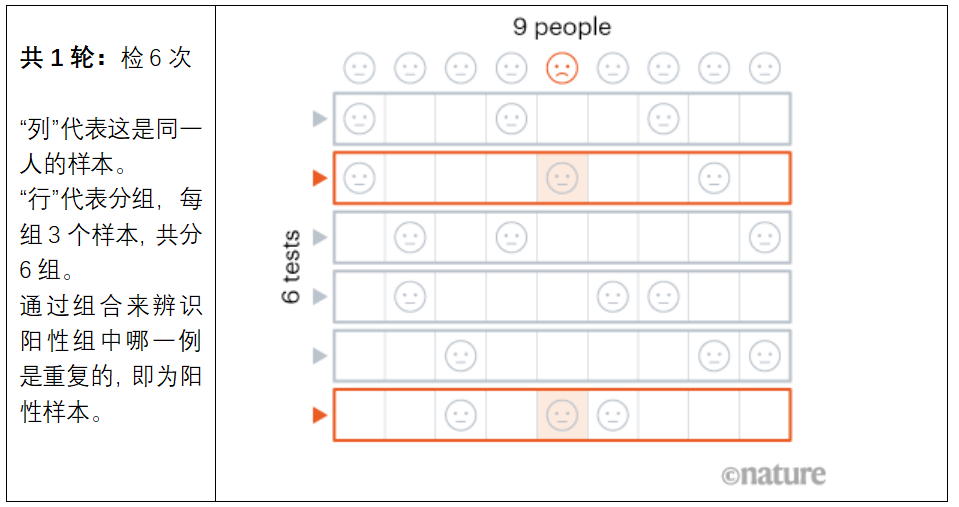
前几种方法都需要分好几轮，而测第2轮必须要等第1轮结果出来，测第3轮要等到第2轮结果出来。轮次越多，等越久越耽误时间。要比病毒更快，科学家于是研究是否能把轮次压缩到极限？印度理工学院的计算机科学家用数学中的柯克曼三元系（Kirkman triples）来完成“一轮搞定”。上图的例子就是如果测9个人，只需要测6次就能找到唯一阳性。

方法一的数学最优问题

方法一个问题，如果样本中的阳性不止一个而且不在同一个分组，第一轮检测到就是3组阳性，第二组3组都要分开检测，实际上检测次数就是27+3=30次。所以，方法一有一个最佳混检的问题。

假如现在有100个人需要检测，使用方法一进行混检，可以5人混检也可以10人混检，更极端的可以1人混检（也就是逐个检测），在给定阳性感染率$p$的前提下，检测的分组的规模多大检测的次数最少？

这个问题的分析可以使用概率中期望的概念，举例来说，如果你花3块钱买彩票，有3种中奖的面值：第一种是10块，中奖率是1/20，第二种是100块，中奖率1/300，第三种10000块，中奖率是1/60000，那么平均来讲，三张彩票你期望得到中奖的金额是

$$ 10* 1/20 + 100* 1/300 + 10000 * 1/60000 = 1/2+1/3+1/6 = 1 $$

所以，用3块钱买了1块钱的期望值，另外两块交了愚人税。将期望值的概念用到这个问题的分析中。假设每次检测$k$个样本为一组，所有样本中的阳性率为$p$，那么使用混检方法一，k个检测样本

  • 没有阳性的概率是$(1-p)^k$，只需要第一轮检测1次即可；
  • 有阳性的概率是$1-(1-p)^k$，那么两轮一共需要检测$k+1$次

所以，总的检测次数的期望是

$$ (1-p)^k + (1-(1-p)^k)(k+1) $$

将这个次数与$k$次相比，如果值小于1，那么说明分组检测有收益，那么问题转化成求

$$ \begin{align} f(k) & = \frac{(1-p)^k + (1-(1-p)^k)(k+1)}{k} \ & = 1/k+1-(1-p)^k\ \end{align} $$

的最小值的问题。依照微积分的知识，函数的极值一般出现在导数为0的地方，求导数为

的解就可以求出$k$的数值。另一种近似解的估值可以通过二项式展开的简化得到

求导得出$k = \frac{1}{\sqrt{p}}$。使用软件绘制函数的图像如下 img

从上面的结果可以看出，在阳性率低于4%时，使用每组5个混检比较合适，但是当阳性率高于20%时，混检已经降低到3个一组，当阳性率为40%时，混检的效率已经不如逐个检测了。

检测结果为阳性的感染概率

引题

参考蒙提霍尔问题 - Wikiwand， 参赛者会看见三扇门，其中一扇门的里面有一辆汽车，选中里面是汽车的那扇门，就可以赢得该辆汽车，另外两扇门里面则都是一只山羊。当参赛者选定了一扇门，主持人会开启另一扇是山羊的门；并问：“要不要换一扇门？

感染概率

居住在金桥居家隔离小区全体人员做核酸检测，很不幸小明第一次核酸检测结果就为阳性，那么小明是否一定感染新冠病毒，感染概率有多大？

这个概率与哪些因素相关？

  • 活动轨迹经过地或者周围环境的新冠病毒浓度水平，他们去过哪些地方？是否是新冠密接？
  • 他们是否打过疫苗？自身的免疫力如何？
  • 检测试剂的质量水平如何？受检测人员的感染时间如何？标本取样时受检测者的配合情况如何？检测人员的流程操作熟练度如何？

假如有人如下的数据，是否可以得到定量的计算

  • 每个人在金桥区域在居家隔离期间的感染新冠的概率是1/10000;
  • 没有感染新冠前提下，新冠试剂检测的**灵敏度(sensitivity)和特异度(specificity)**均为99%（具体的定义参考下图，真的感染之后被判定为阳性的概率，和没有感染被判定为阴性的概率，具体的定义可以参考后面的示意图）

推导贝叶斯定理

对于这个问题的计算可以从如下朴素的定义开始，

受测者检测为阳性后感染新冠的概率，等于检测结果为阳性的感染新冠病毒的人数与所有检测为阳性人数之比

朴素推导

  1. 假如金桥地区有10000个居民，根据感染概率，其中真实感染新冠的有10个，剩下的9990个居民实际是没有感染新冠的，也就是在没有其他信息前提下已知该地区的居民的感染率是1/1000；
  2. 在较为理想的情况下，排除其他检测操作不规范的等因素，我们假设试剂检测性能，在100个真实感染病例中可以检测出99个为阴性，1个为阳性（灵敏度是99%），同样的，100个没有真实没有感染的居民中检测出来1个阳性，其他的99个为阴性（特异度是99%)

根据上面的假设，计算

从上面的公式可以看出假阳性人数占比较高，就会造成检测结果的不准确性，所以要提高阳性检测的准确率就需要尽量降低假阳性的病例，

  1. 提高试剂检测的特异度，如果将特异度提高到100%，那么就不会有没有感染的人被判定为假阳性，准确率是100%；
  2. 如果真正感染的人数比例较高，那么真阳性就可以占有比较大的份额，检测结果更可信。

还有一个方法就是重复测试，如果上述条件不变，根据贝叶斯公式推导可以得到，两次复检均为阳性患病的的概率可以提高到90%。

理论推导

用数学的语言描述就是，如果用事件$D$表示感染新冠，事件$+$表示检测为阳性，那么

$$ Pr(D|+) = \frac{Pr(+D)}{Pr(+)} $$

其中

  • $P(D) = \frac{真正感染的人数}{检测为阳性的人数}$ 表示感染新冠病毒的概率，这里是先验概率，表示在看到化验结果之前的感染的概率，称为先验概率，这个值的大小与金桥地区的感染人数，受测者在金桥地区的活动轨迹，受测者自身是否佩戴口罩等环境与受测者自身的因素相关，测算一般比较复杂，可以通过历史统计或者理论推理得到，这里的值就是前面的1/10000
  • $P(D|+)$表示检测阳性的情况下，感染新冠的概率，也是需要估算的目标值
  • $Pr(+D) = \frac{真正感染并且检测为阳性的人数}{总人数}$ 表示感染新冠，并且检测是阳性的概率
  • $Pr(+) = \frac {真正感染并且检测为阳性的人数 + 没有感染并且检测为阳性的人数}{总人数}$表示所有受测者检测为阳性的概率

根据全概率公式

$$ Pr(AB) = Pr(A|B)Pr(B) $$

可以得到$Pr(+D) = Pr(+|D)Pr(D)$，带入到上面的式子可以得到

$$ \begin{align} Pr(D|+) & = \frac{Pr(+D)}{Pr(+)} \ & = \frac{Pr(+|D)Pr(D)}{Pr(+)} \ \end{align} $$

这个就是贝叶斯定理。

继续上面公式的推算过程，

$$ \begin{align} Pr(D|+) & = \frac{Pr(+D)}{Pr(+)} \ & = \frac{Pr(+|D)Pr(D)}{Pr(+)} \end{align} $$

其中，$Pr(+|D)$表示感染新冠的情况下被检测出为阳性的概率，也就是检测试剂的灵敏度，这个值是0.99，一般这一项称为$+$的后验概率。

对于$Pr(+)$可以继续使用全概率公式$Pr(+) = Pr(+|D)Pr(D) + Pr(+|\bar D)P(\bar D)$，检测阳性的人数比例，等于感染新冠的人数的检测阳性的概率与没有感染新冠的检测阳性的概率，所以最终的结果是

其中，

  • $Pr(+|\bar D)$ 表示未感染新冠的情况下被检测出为阳性的概率，这个值是0.01，是1 - 灵敏度的概率。
  • $Pr(\bar D)$就是在金桥地区不会感染的概率，为1 - 1/10000 = 9999 / 10000

理解贝叶斯定理

可以参考理解贝叶斯定理的文章。

参考资料

  1. 蒙提霍尔问题 - Wikiwand
  2. 核酸检测准确率有多高？为什么阴性结果有效期定在7天之内？
  3. [法] 黄黎原著,方弦译.贝叶斯的博弈：数学、思维与人工智能.人民邮电出版社.2010:32. 得到电子书：https://d.dedao.cn/Dx3bkkZw5l51Et9R
  4. 七种国产新型冠状病毒核酸检测试剂盒的一致性和检出能力评价研究 - 中华检验医学杂志
  5. 灵敏度和特异度 - Wikiwand
  6. 这些因素或导致“假阳、假阴”，新冠防控利器如何更精准|RNA_新浪财经_新浪网
  7. 2019新型冠状病毒特异抗体检测 "假阳性 "原因分析及对策 - 中华检验医学杂志
  8. 搜索天蝎号核潜艇
  9. Bayesian search theory - Wikiwand
  10. David L. Wallace, statistician who helped identify Federalist Papers authors, 1928-2017
  11. 【科普】核酸检测的原理到底是什么？为什么会出现假阴性？_图片新闻_汕头市卫生健康局（中医药局）

全文完🚀

Bayesian
Licensed under CC BY-NC-SA 4.0
comments powered by Disqus